Thomas' Calculus - 2. Limits and Continuity

1. Limit of a Function

극한을 계산할 때 필요한 기본적인 극한의 성질들이 있는데 이를 Limit Laws라고 부른다. 아래의 성질은 변수 x가 무한으로 갈 때도 성립한다.

 

극한은 아래와 같이 정의한다. x가 c로 갈 때 함수 f(x)의 극한값이 L이라는 사실은 아래의 절차를 통해 보일 수 있다. 1) f(x)와 L의 차의 절댓값이 임의의 양수 ε보다 작게 만드는 x 값의 interval (a, b)를 구한다. 2) (a, b)에 포함되는 interval (c-δ, c+ δ)를 만족하는 적당한 양의 실수 δ를 찾는다.

 

x가 무한대로 가는 경우의 극한도 아래와 같이 정의할 수 있다.

 

그리고 극한값이 하나의 값에 수렴하는 것이 아니라 무한대로 발산할 수도 있다.

 

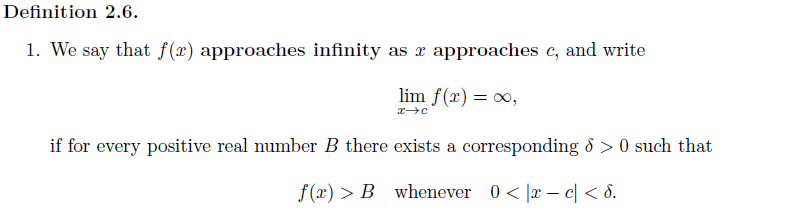
2. Asymptotes of Graphs

그래프를 sketch할 때 asymptotes를 찾는 것은 중요하다. x가 ±무한대로 갈 때 f(x)가 유한한 값 b로 수렴할 경우 horizontal asymptote는 y=b가 된다. 

 

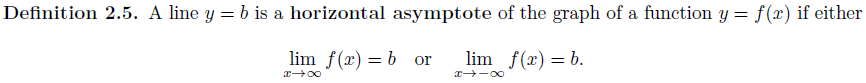
반대로 vertical asymptote는 x가 특정한 값 a에 무한히 가까워질 때 f(x)가 ±무한대로 발산할 경우 x=a가 된다.

 

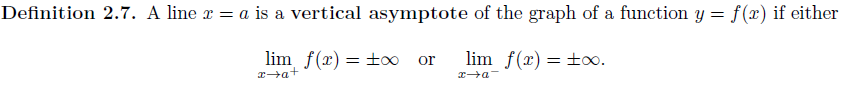
분자의 degree가 분모의 degree보다 1만큼 큰 rational function의 그래프는 oblique(또는 slant line asymptote)를 가진다. 아래 Example을 보자.

 

위 Example에서 볼 수 있다시피 분모의 degree가 분자의 degree보다 1이 큰 경우 그 함수는 x에 대한 선형함수와 나머지 부분으로 나눌 수 있다. 위 Example에서 x가 무한대로 갈 때, 그리고 2로 한없이 가까워질 때 dominant term은 각각 선형 부분과 나머지 부분이 된다.

 

3. Continuity

f(x)가 x=c에서 continuous한지를 보이기 위해서 아래의 절차를 거치면 된다. 대부분의 함수는 continuous하지만 일부 함수는 그렇지 않다.

 

함수 f가 어떤 closed interval에서 continuous하다면 아래의 Intermediate Value Theorem을 만족한다.