Thomas' Calculus - 3. Derivatives

1. The Derivative as a Function

x가 아주 조금 움직일 때 함수값의 변화를 derivative라고 한다. Derivative는 x에 대한 함수로 표현할 수 있다.

 

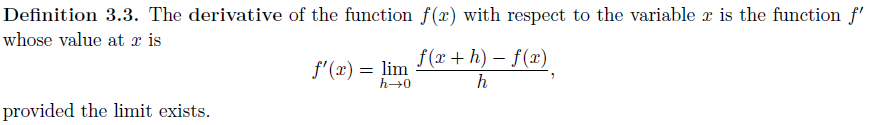
점 x에서 어떤 함수 f의 derivative가 존재할 때 f는 x에서 differentiable하다고 말한다. Derivative를 계산하는 과정을 differentiation이라고 부르기로 한다. 함수 f의 derivative는 f' 또는 d/dx로 주로 표기한다.

 

2. Differential Rules

아래는 다양한 Differential Rule이다. 모두 derivative의 정의로 증명할 수 있다. 다만 Power Rule에서 n이 rational number가 아닌 경우 현 단계에서 증명할 수는 없으나 추후 exponential function을 정의하고 난다면 증명할 수 있을 것이다.

 

 

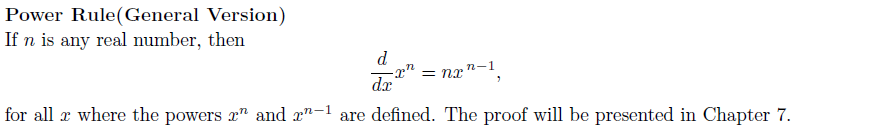
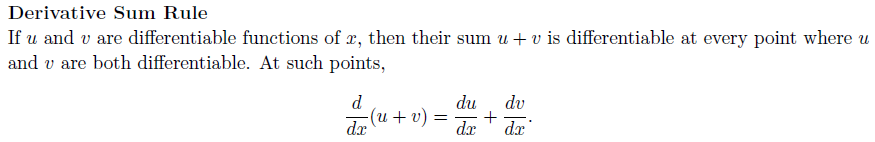
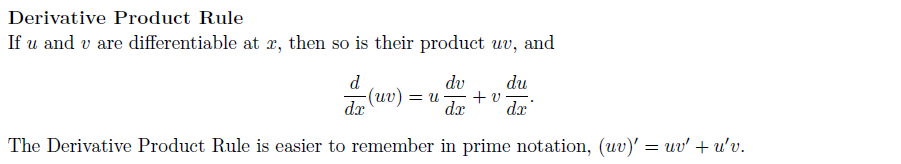
3. Derivatives of  Trigonometric Functions

Trigonometric function의 derivative는 주기적인 변화를 기술할 때 유용하게 쓰인다.

 

4. The Chain Rule

Chain Rule의 증명은 아래에 나온다.

 

5. Linearization and Differentials

미분을 배우는 가장 중요한 이유는 복잡한 함수의 변화값을 linear approximation을 이용해서 쉽게 알아내려는 것이다. 그렇기에 아래의 linearization의 정의가 중요하다.

 

그리고 differential의 개념이 등장한다. 미분의 라이프니츠 표기법인 dy/dx는 비율이 아니다. 하지만 새로운 두 변수 dx와 dy의 비율이 존재할 때 그 비율은 derivative와 같도록 두 변수 dx와 dy를 정의할 수 있다.

 

직관적으로 이해해 보자면 다음과 같다. dx는 x값의 매우 작은 변화를 의미한다. 우리가 알고 싶은 것은 x가 dx만큼 움직였을 때 함수값이 얼마나 변하는지다. 그러나 어떤 함수는 그 값을 계산하기조차 어렵다. 이 경우 대안적으로 선형함수인 x 값에서의 standard linear approximation의 변화를 측정하는 것이다. x가 dx만큼 움직였을 때 이 선형함수의 함수값의 변화가 바로 dy가 되는 것이다.

 

따라서 다음과 같이 쓸 수 있다.

 

6. Proof of the Chain Rule

이는 실제 y값의 변화를 다음과 같이 error term이 추가된 형태로 쓸 수 있음을 시사한다.

 

다음은 Chain Rule의 증명이다.